什么是二分查找
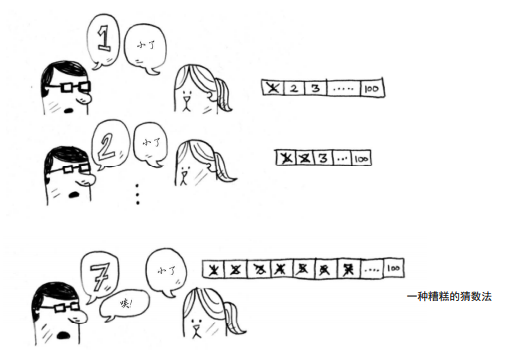
下面的示例说明了二分查找的工作原理。我随便想一个1~100的数字。你的目标是以最少的次数猜到这个数字。你每次猜测后,我会说小了、大了或对了。
- 假设你从1开始依次往上猜,猜测过程会是这样。这是简单查找,更准确的说法是傻找。每次猜测都只能排除一个数字。如果我想的数字是99,你得猜99次才能猜到!
-
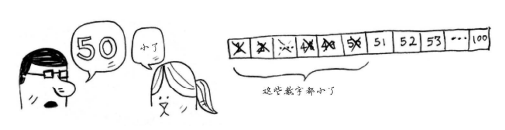
下面是一种更佳的猜法。从 50 开始。
小了,但排除了一半的数字!至此,你知道1~50都小了。接下来,你猜75。
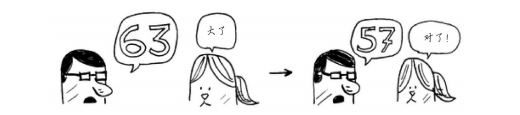
大了,那余下的数字又排除了一半!使用二分查找时,你猜测的是中间的数字,从而每次都 将余下的数字排除一半。接下来,你猜63(50和75中间的数字)。
这就是二分查找,你学习了第一种算法!每次猜测排除的数字个数如下。
不管我心里想的是哪个数字,你在7次之内都能猜到,因为每次猜测都将排除很多数字!
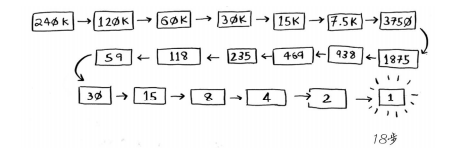
假设你要在字典中查找一个单词,而该字典包含240 000个单词,你认为每种查找最多需要多少步? 如果要查找的单词位于字典末尾,使用简单查找将需要240 000步。使用二分查找时,每次 排除一半单词,直到最后只剩下一个单词。
因此,使用二分查找只需18步——少多了!一般而言,对于包含n个元素的列表,用二分查 找最多需要log2n步,而简单查找最多需要n步。
什么是二叉树
树
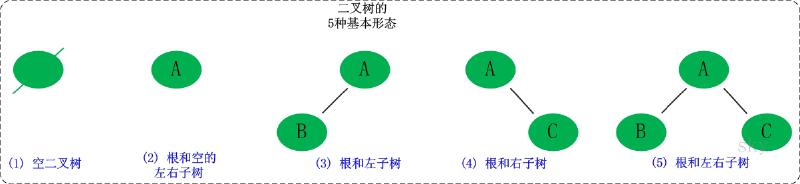
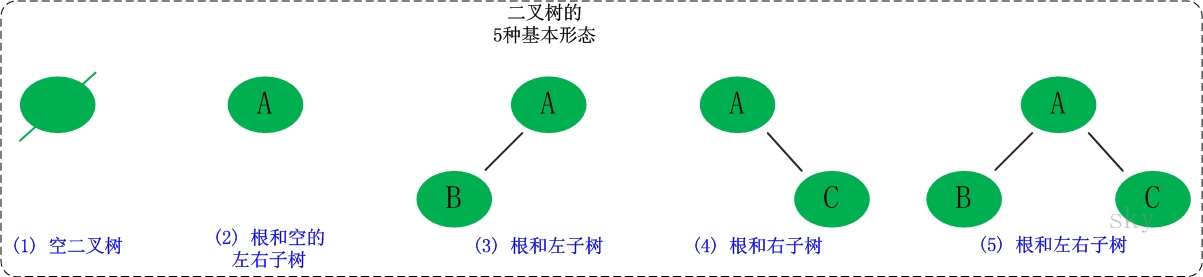
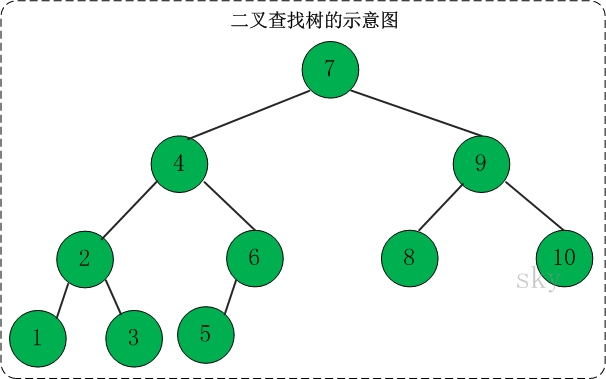
如图中第5个实例所示,这是一棵基本的二叉树;二叉树由根(根节点)和左子树(左节点)、右子树(右节点)组成,A节点为B和C节点的父节点。
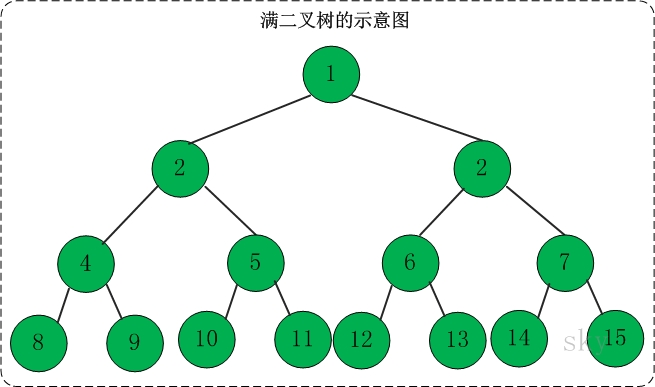
满二叉树
满二叉树有以下特性
- 二叉树的所有叶子节点(末节点)到根节点层次都需要相等。(也可以说:高度为h,并且由2{h} –1个结点的二叉树,被称为满二叉树。)
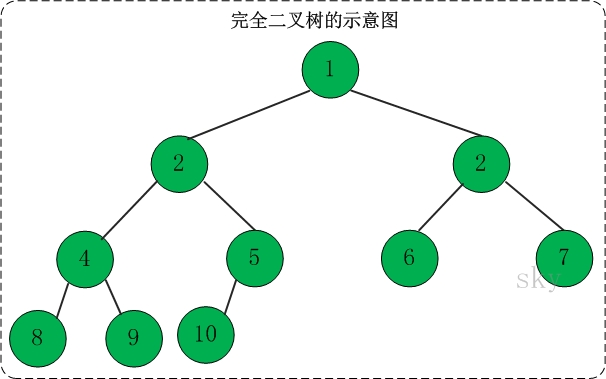
完全二叉树
完全二叉树有以下特性
- 叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
- 一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
二叉查找树
二叉查找树有以下特性
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 任意节点的左、右子树也分别为二叉查找树
- 没有键值相等的节点
从二分查找到二叉查找树再到红黑树
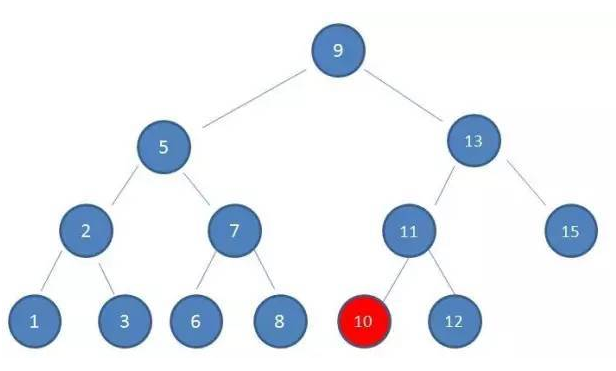
如图所示,这是棵二叉查找树,我们需要从根节点9开始,查找找到10,过程是如何的呢:
- 由于10 > 9,因此查看右孩子13
- 由于10 < 13,因此查看左孩子11
- 由于10 < 11,因此查看左孩子10,发现10正是要查找的节点
很明显,二叉查找树的查找方式正式借用了二分查找的思想。
插入节点的时候也是借用了该思想,还是如图所示我们插入10,过程如下:
- 由于10 > 9,因此查看右孩子是否为空,不为空继续向下查找
- 由于10 < 13,因此查看左孩子是否为空,不为空继续向下查找
- 由于10 < 11,因此查看左孩子是否为空,发现正好为空,那么设置11的左为10
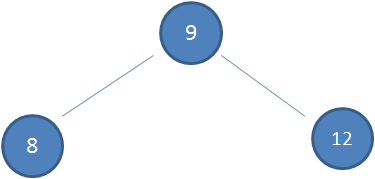
但是,二叉查找还是存在缺陷的,假设我们设置初始二叉查找树为以下结构:
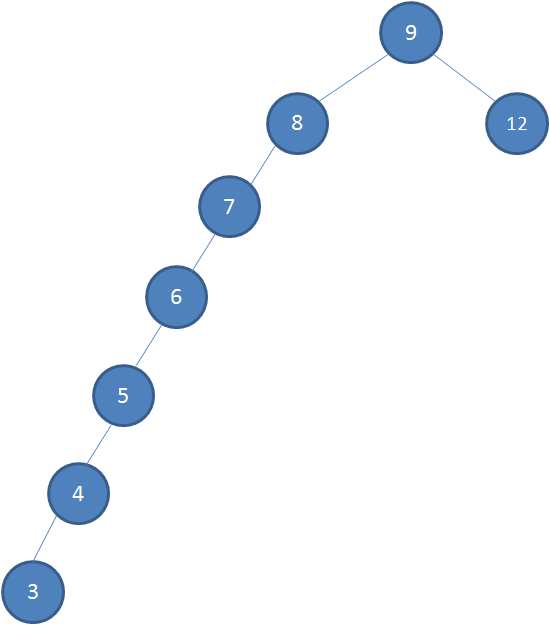
这时候我们按指定顺序插入以下数值:7,6,5,4,3。依照二叉查找树的特性,结果会变成什么样呢?
这样的形态虽然也满足二叉查找树的特性,但是查找性能大打折扣,几乎成了线性,甚至考虑维护因素还不如线性。
为了解决二叉查找树这一缺陷,红黑树孕育而生。
什么是红黑树
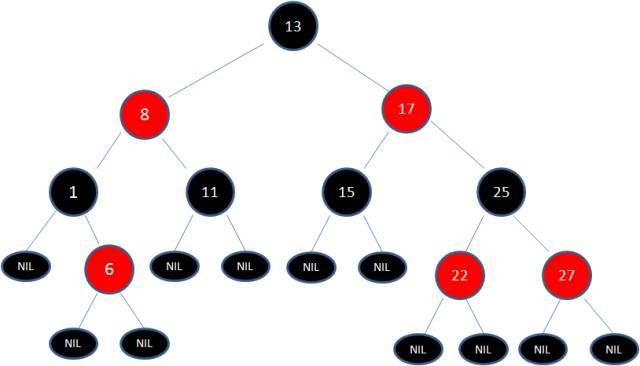
红黑树是一种自平衡二叉查找树,除了满足二叉查找树的基本特性,它还有以下特性:
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶子节点都是黑色的空节点(NIL节点)。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
下图中这棵树,就是一颗典型的红黑树:
红黑树写法教程参考:https://www.jianshu.com/p/e136ec79235c
对参考文章中的一些补充:
红黑树代码如下(Ps:删除存在问题,没有处理好为叶节点且为黑色节点的删除处理)
List<Node> nodes = new List<Node>();
private const int R = 0;
private const int B = 1;
/// <summary>头节点</summary>
Node _root = null;
public class Node
{
public int data;//节点数据
public int color = R;
public Node left { get; private set; }//左子节点
public Node right { get; private set; }//右子节点
public Node parent { get; private set; }//父节点
public void SetParent(Node node)
{
this.parent = node;
}
public void SetLeft(Node node)
{
if (node != null)
{
node.parent = this;
}
this.left = node;
}
public void SetRight(Node node)
{
if (node != null)
{
node.parent = this;
}
this.right = node;
}
public Node(int data)
{
this.data = data;
}
/// <summary>
/// 获取爷爷节点
/// </summary>
/// <returns></returns>
public Node GetGrandpa()
{
if (parent != null)
{
return parent.parent;
}
return null;
}
/// <summary>
/// 获取叔叔节点
/// </summary>
/// <returns></returns>
public Node GetUncle()
{
if (parent != null && parent.parent != null)
{
if (parent.parent.left == parent)
{
return parent.parent.right;
}
else
{
return parent.parent.left;
}
}
return null;
}
/// <summary>
/// 是左节点
/// </summary>
/// <returns></returns>
public bool IsLeft()
{
if (parent != null && parent.left == this)
return true;
else
return false;
}
}
/// <summary>
/// 插入
/// </summary>
/// <param name="root">当前判定的根节点</param>
/// <param name="data">插入的数据</param>
public void Add(int data, Node root = null)
{
//——情况1:如果是首次插入
if (root == null)
{
//——情况1.1:如果是空树
if (_root == null)
{
_root = new Node(data);
nodes.Add(_root);
Check(_root);
return;
}
else
{
Add(data, _root);
}
}
//——情况2:如果是首次插入
else
{
//——情况2.1:如果大于插入值
if (root.data < data)
{
//——情况2.1.1:如果右节点为空
if (root.right == null)
{
Node node = new Node(data);
nodes.Add(node);
root.SetRight(node);
Check(node);
}
else
{
Add(data, root.right);
}
}
//——情况2.2:如果小于或等于插入值
else
{
//——情况2.2.1:如果左节点为空
if (root.left == null)
{
Node node = new Node(data);
nodes.Add(node);
root.SetLeft(node);
Check(node);
}
else
{
Add(data, root.left);
}
}
}
}
/// <summary>
/// 插入节点
/// </summary>
/// <param name="node"></param>
public void Check(Node node)
{
//如果插入节点没有父节点(即根节点)
if (node.parent == null)
{
_root.color = B;
}
else
{
//如果父节点为红色
if (node.parent.color == R)
{
Node u = node.GetUncle();
//如果叔叔节点存在,且为红色
if (u != null && u.color == R)
{
Node g = node.GetGrandpa();
//设置爷爷节点为红色
g.color = R;
//叔叔节点和父节点为黑色
g.left.color = g.right.color = B;
//设置爷爷节点为当前节点。
Check(g);
}
//如果叔叔节点不存在,或者为黑色
else
{
//如果父节点是左节点
if (node.parent.IsLeft())
{
//如果当前节点是左节点
if (node.IsLeft())
{
node.parent.color = B;
node.GetGrandpa().color = R;
RightRotate(node.GetGrandpa());
}
//如果当前节点是右节点
else
{
Node p = node.parent;
LeftRotate(p);
//设置“旋转”之前父节点为当前节点。
Check(p);
}
}
//如果父节点是右节点
else
{
//如果当前节点是右节点
if (!node.IsLeft())
{
node.parent.color = B;
node.GetGrandpa().color = R;
LeftRotate(node.GetGrandpa());
}
//如果当前节点是左节点
else
{
Node p = node.parent;
RightRotate(p);
//设置“旋转”之前父节点为当前节点。
Check(p);
}
}
}
}
//如果父节点为黑色
else
{
return;
}
}
}
/// <summary>
/// 左旋
/// </summary>
/// <param name="node"></param>
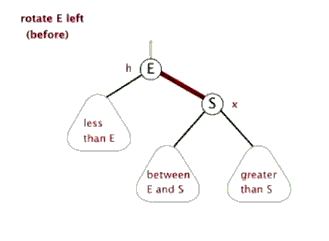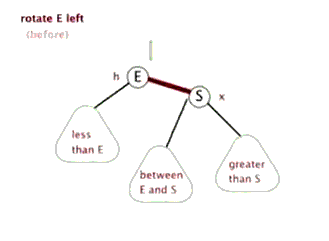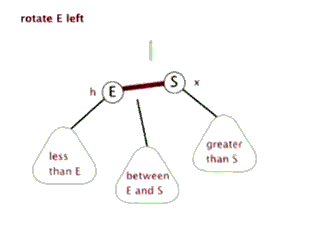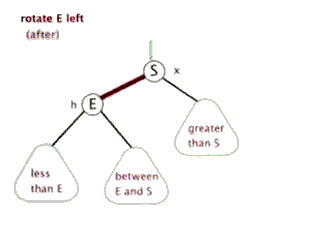
public void LeftRotate(Node node)
{
//原始父节点
Node p = node?.parent;
Node e = node;
Node s = node.right;
Node b = s?.left;
s.SetLeft(e);
e.SetRight(b);
if (p != null)
{
if (p.left == e)
{
p.SetLeft(s);
}
else
{
p.SetRight(s);
}
}
else
{
s.SetParent(null);
_root = s;
}
}
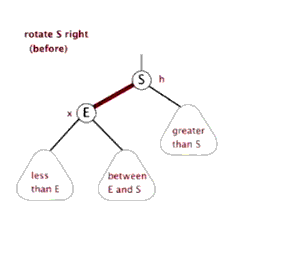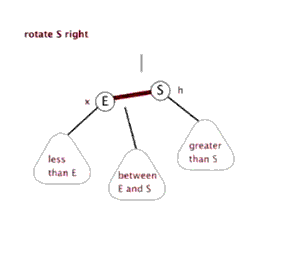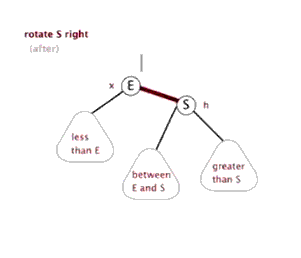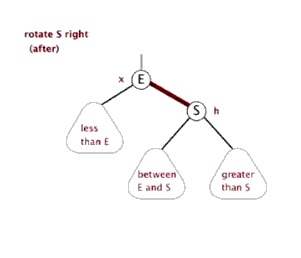
/// <summary>
/// 右旋
/// </summary>
/// <param name="node"></param>
public void RightRotate(Node node)
{
Node p = node?.parent;
Node s = node;
Node e = node.left;
Node b = e?.right;
s.SetLeft(b);
e.SetRight(s);
if (p != null)
{
if (p.left == s)
{
p.SetLeft(e);
}
else
{
p.SetRight(e);
}
}
else
{
e.SetParent(null);
_root = e;
}
}
/// <summary>
/// 删除
/// </summary>
/// <param name="data"></param>
public void Remove(int data)
{
Node node = _root;
while (true)
{
if (node == null)
return;
if (data == node.data)
break;
if (data > node.data)
node = node.right;
else
node = node.left;
}
Remove(node);
}
/// <summary>
/// 删除节点
/// </summary>
/// <param name="node"></param>
void Remove(Node node)
{
///2131321231
///
//1.没有子节点的情况
if (node.left == null && node.right == null)
{
//1.1为根节点情况
if (node.parent == null)
{
_root = null;
}
//1.2不为根节点情况
else
{
if (node.parent.left == node)
node.parent?.SetLeft(null);
else
node.parent?.SetRight(null);
}
}
//2.1 只有一个右子节点情况
else if (node.left == null && node.right != null)
{
if (node.IsLeft())
node.parent?.SetLeft(node.right);
else
node.parent?.SetRight(node.right);
}
//2.2 只有一个左子节点情况
else if (node.left != null && node.right == null)
{
if (node.IsLeft())
node.parent?.SetLeft(node.right);
else
node.parent?.SetRight(node.right);
}
//3.两个节点都有的情况
else
{
//获取删除节点的替代节点
Node replace = node.right;
while (replace.left != null)
{
replace = replace.left;
}
Replace(replace);
Node p = node.parent;
Node l = node.left;
Node r = node.right;
if (replace.IsLeft())
replace.parent.SetLeft(node);
else
replace.parent.SetRight(node);
if (p != null)
{
if (p.left == node)
p.SetLeft(replace);
else
p.SetRight(replace);
}
else
{
_root = replace;
}
node.SetLeft(replace.left);
node.SetRight(replace.right);
replace.SetLeft(l);
replace.SetRight(r);
Remove(node);
}
}
/// <summary>
/// 替代方法
/// </summary>
/// <param name="replace">替代节点</param>
Node Replace(Node replace)
{
//3.1 替代节点是红色节点
if (replace.color == R)
{
replace.color = B;
}
//3.2 替代节点是黑色节点
else
{
//3.2.1 替代节点是左节点
if (replace.IsLeft())
{
//3.2.1.1 替代节点的兄弟节点是红色
if (replace.parent.right.color == R)
{
replace.parent.right.color = B;
replace.parent.color = R;
LeftRotate(replace.parent);
//后处理
return Fun_2_1_2_3();
}
//3.2.1.2 替代节点的兄弟节点是黑色
else
{
//3.2.1.2.1 替代节点的兄弟节点的右节点是红色
if (replace.parent.right.right.color == R)
{
replace.parent.right.color = replace.parent.color;
replace.parent.color = B;
replace.parent.right.right.color = B;
LeftRotate(replace.parent);
}
//3.2.1.2.2 替代节点的兄弟节点的右节点是黑色
else
{
//3.2.1.2.2.1 替代节点的兄弟节点的左节点是红色
if (replace.parent.right.left.color == R)
{
replace.parent.right.color = R;
replace.parent.right.left.color = B;
RightRotate(replace.parent.right);
//后处理
Fun_2_1_2_1();
}
//3.2.1.2.2.2 替代节点的兄弟节点的左节点是黑色
else
{
replace.parent.right.color = R;
//重新替换 replace.parent;
return Replace(replace.parent);
}
}
}
}
//3.2.2 替代节点是右节点
else
{
//3.2.2.1 替代节点的兄弟节点是红色
if (replace.parent.left.color == R)
{
replace.parent.left.color = B;
replace.parent.color = R;
RightRotate(replace.parent);
//后处理
Fun_2_2_2_1();
}
//3.2.2.2 替代节点的兄弟节点是黑色
else
{
//3.2.2.2.1 替代节点的兄弟节点的左节点是红色
if (replace.parent.left.left.color == R)
{
replace.parent.left.color = replace.parent.color;
replace.parent.color = B;
replace.parent.left.left.color = B;
RightRotate(replace.parent);
}
//3.2.2.2.2 替代节点的兄弟节点的左节点是黑色
else
{
//3.2.2.2.2.1 替代节点的兄弟节点的右节点是红色
if (replace.parent.left.right.color == R)
{
replace.parent.left.color = R;
replace.parent.left.right.color = B;
LeftRotate(replace.parent.left);
//后处理
return Fun_2_2_2_3();
}
//3.2.2.2.2.2 替代节点的兄弟节点的右节点是黑色
else
{
replace.parent.left.color = R;
//重新替换计算 replace.parent
return Replace(replace.parent);
}
}
}
}
}
return replace;
Node Fun_2_1_2_3()
{
replace.parent.right.color = R;
//重新替换 replace.parent;
return Replace(replace.parent);
}
void Fun_2_1_2_1()
{
replace.parent.right.color = replace.parent.color;
replace.parent.color = B;
replace.parent.right.right.color = B;
LeftRotate(replace.parent);
}
Node Fun_2_2_2_3()
{
replace.parent.left.color = R;
//重新替换计算 replace.parent
return Replace(replace.parent);
}
void Fun_2_2_2_1()
{
replace.parent.left.color = replace.parent.color;
replace.parent.color = B;
replace.parent.left.left.color = B;
RightRotate(replace.parent);
}
}